One more quick comment on the Political Survey -- I've now written some code to estimate which of the eigenvectors are significant. The basic idea is that we generate synthetic data using the marginal distributions for each statements -- that is, like the data which would have been produced by the same number of respondents as have completed the real survey, but as if their answers to any one question were unrelated to all the others; and having done that, we perform the principal components analysis on the synthetic data. The idea here is that we can compare the eigenvalues from the synthetic data to the eigenvalues from the real data. If the real eigenvalue is significantly larger than the one from the synthetic data, it likely represents real variation in the data; otherwise, random variation.
Here's how they turn out:
| n | real data eigenvalue | synthetic data eigenvalue | caricature |
|---|---|---|---|
| 0 | 12.770 | 4.243 | Daily Mailism |
| 1 | 4.863 | 4.202 | Social Liberalism |
| 2 | 3.860 | 3.997 | ? |
| 3 | 3.569 | 3.766 | |
| 4 | 3.187 | 3.603 | |
| 5 | 2.838 | 3.440 |
-- suggesting that the first two eigenvectors are significant, but none of the others. It's possible that this could change with more data, but I don't really expect it to. So the first actual result is that two axes are sufficient to describe the data we have so far.
The next check I need to do is to determine how well-constrained the eigenvectors are. More thoughts on that later.
And more flaming
I seem to have been having an argument with Peter Cuthbertson (see end of page), which is pretty futile; but it has provoked me into producing a toy model of the UK population, which I might say something about at some later stage. I was using this to calculate the ratio of working age people to pensioners, on the basis that Cuthbertson apparently doesn't believe that immigration can affect this. Anyway, the resulting graph:
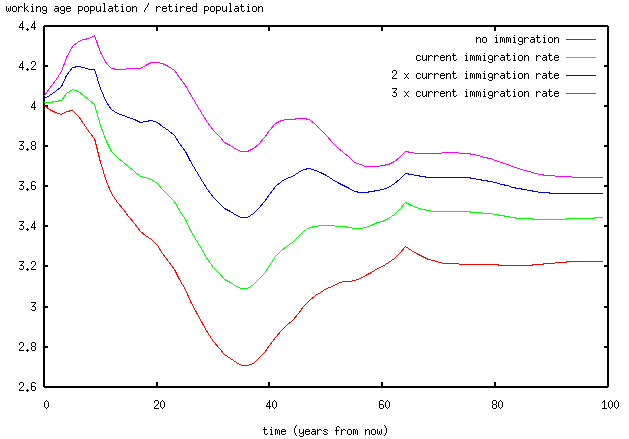
The model itself is pretty simple; you can get the code here.