So, a couple of days ago I mentioned a simple model of the UK population which I've produced to inform my views on the upcoming `pensions crisis'. (Why I wanted to do that is another story, best not dwelt on here....) Herewith some thoughts on the subject:
Background
Current pensions for retired people are funded out of the current output of the economy, because most of the goods and services which people consume in their retirement -- food, medical treatment, transport, etc. -- are perishable or can't be stored. So, there must be an `intergeneration transfer' of wealth from those who are presently working to those who are presently retired. If the number of workers producing output falls relative to the number of retired people, then there will be a shortfall in pensions. Such a fall in the ratio of workers to pensioners is expected to occur in the relatively near future, as people from the `baby boom' generation reach retirement age.
Superficially, it might seem that `fully funded' pensions, where each worker saves money to spend in their retirement, get around this problem. In fact, this is not the case; there's good discussion of why not in this paper by John Eatwell and this IMF paper by Nicholas Barr. To precis, imagine that you invest your pension payments in some sort of financial instrument (for instance, equities). The price of those shares is determined by the demand for them. Fast-forward to your retirement; now you need to sell your investments. Again, their price is determined by the demand for them, and that is determined by the number of people investing in pensions at the time of your retirement. If the number of workers saving for their pensions is smaller when you retire than at the time you are selling your investments, then your investments will drop in value. Similarly, if you save cash, then the increased spending by retired people will lead to inflation at the time that you retire (see pp8--9 of Barr).
The simple way to express this is through a model of output and pensions saving. Clearly, pension payments = workers' savings + tax spent on pensions; or, writing P for the average pension, N for the number of pensioners, S for the savings rate, T for the tax rate, Y for average annual output per worker, and W for the number of workers, PN = (S + T)YW. (Eatwell p4.)
The average pension that society can afford, P, is then given by (S + T)YW / N; critically, it depends on W / N, the ratio of workers to pensioners in the population. (It will also change with the sum of pensions savings and tax spent on pensions, and with the average output per worker, but shifting between savings and tax makes no difference.)
How will the ratio W / N vary over time?
A simple population model
Formally, model the population of the country as a density function p(a); a is age, and p(a)da tells us the number of people between the ages of a and (a + da). (Note that in principle we should model the male and female populations independently, but for a simple model we can just assume that half the population is male and the other half female.) The evolution of the population is then described by (d/dx are partial derivatives; HTML is lousy for maths...)
dp(a)/dt = - dp/da - d(a)p + i(a)
where d(a) is the death rate per person per unit time, and i(a) is net immigration per unit time. (Typically this is how the figures are quoted, and intuitively we expect the death rate to be per person but not the immigration rate.) We then need another equation to represent the birth of children:
dp(0)/dt = Integral[b(a)p(a) / 2, 0, infinity] - dp(0)/da - d(0)p(0) + i(0)
where b(0) is the birth rate per woman per unit time; the factor of two is there because only half the population are women.
The parameter of interest for the pensions problem -- the ratio of working-age to retired people -- is then given by
W / N = Integral[p(a), aw, ar] / Integral[p(a), ar, infinity]
where aw is the age people start working (18) and ar is the retirement age (65).
(Slightly less formally, imagine the population of the country divided by age into buckets, one for each year of age. The contents of the bucket next year is the population of the bucket one year younger minus the number of people who died plus the number of people who immigrated. For the very first bucket -- age zero -- we also add the number of people born. Since all the available data are done in terms of one-year -- or larger -- age buckets, we may as well just use a model which works on one-year buckets.)
Data on the initial p(a) -- the current population pyramid -- is summarised from the 2001 Census; National Statistics also provides data for death rates, birth rates, and immigration rates. Some of these rates are given over age ranges of greater than one year; in these cases we assume that the functions are uniform over each interval. (A priori, there's no reason to do otherwise.)
Given this, we can use the model to make predictions of what the population will do in the future. We make the simplifying assumption that birth, death and immigration rates do not vary with time. Obviously they will, but again it is best to make the simplest possible assumptions.
(If you're interested, you can get the code for the model and the script which makes the plots below.)
Illustrative results
Here are population pyramids, with rates of birth, death and immigration fixed at current levels:
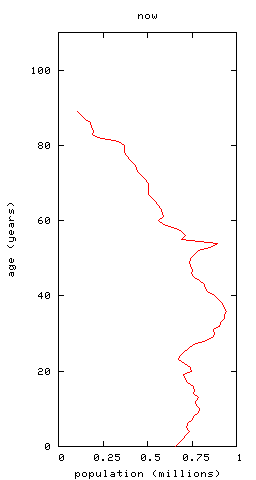
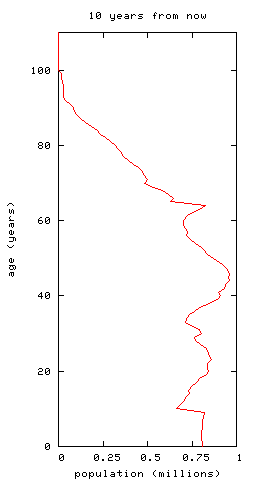
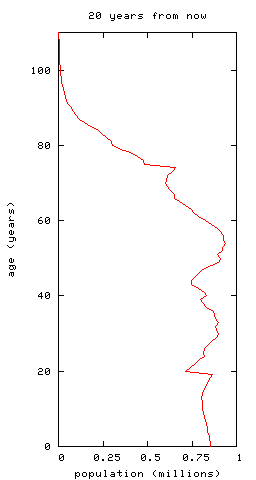
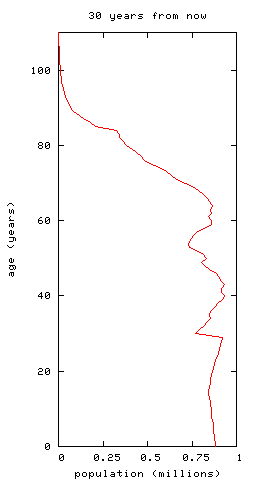
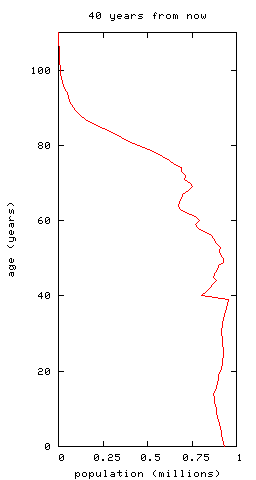
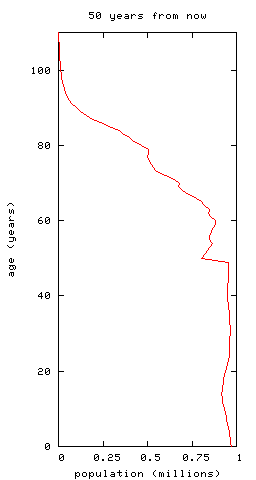
-- you can see the bulge of people now aged 30--40ish moving up to retirement age. To illustrate this further, plot the ratio of workers to pensioners we predict, again with fixed birth, death and immigration rates:
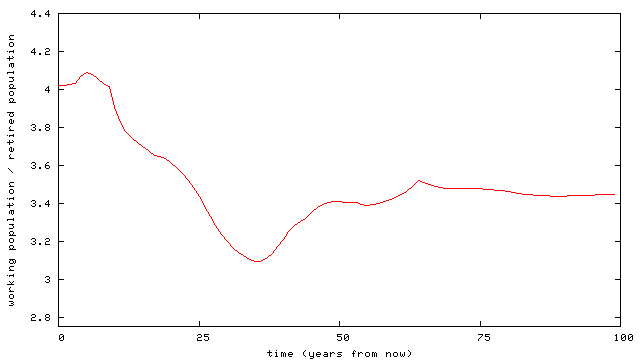
Presently, there are 4.02 times as many workers as pensioners. This will drop by 23% to 3.09 in 35 years' time, meaning that -- at current rates of output -- average pensions will also drop by 23%. (This is slightly larger than the prediction in the Eatwell paper, which is about 19%, but of the same order.) It will then rise again, but -- in the steady-state model here -- it will not again reach anything like its current value, instead settling at 3.44, about 14% below today's value.
Two ways to improve the situation are to increase birth rates or to allow more working-age immigrants into the country. What effects do these have?
First, birth rates:
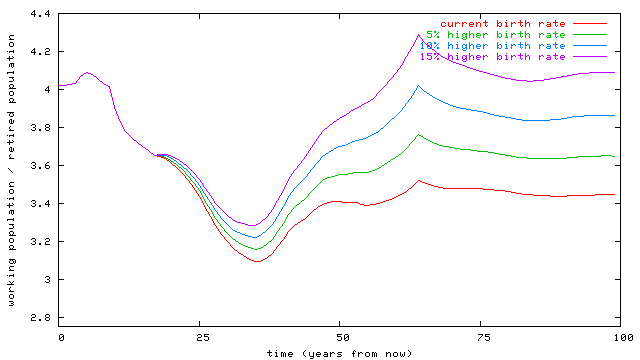
Note that this has no effect until today's children start to enter the workforce, and children only gradually feed into the workforce. We can plot the worst workers/pensioners ratio in the trough as a function of increase in birth rate:
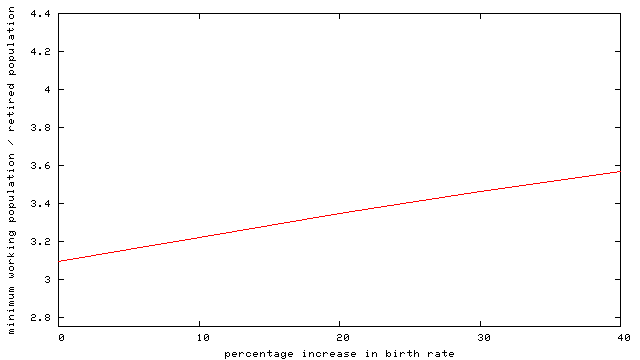
-- even by increasing birth rates by 40% -- which is unreasonable -- we can't keep the workers/pensioners ratio at or above its current value.
Second, immigration:
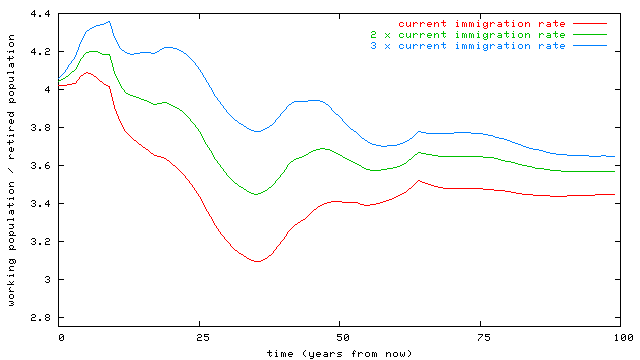
As we increase the immigration rate, the trough becomes shallower and the long-term ratio rises. Plotting the depth of the trough as a function of immigration rate:
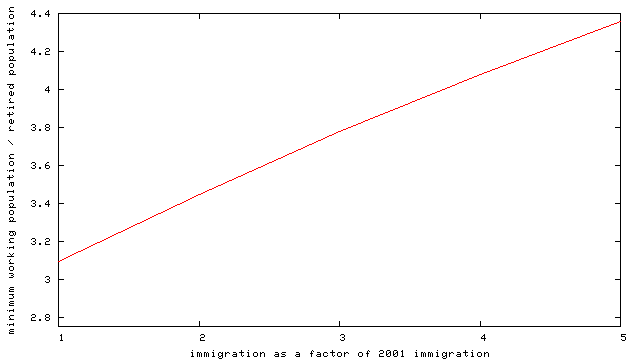
-- we see that increasing immigration from its current rate (about 180,000 per year) to three to four times that value will effectively eliminate the thirty-five year trough in the workers/pensioners ratio. There will then be another trough about sixty years hence, but (a) it's not very deep; and (b) it's very questionable to extend these predictions so far into the future.
What about economic growth?
So far we've ignored this. Clearly, if productivity (output per worker) grows, then the situation improves, since fewer workers can support the same number of pensioners, keeping pensions at their current level in real terms. At current rates of birth, death and immigration, we need productivity growth of 23% over 35 years, or about 0.5% per year, to keep pensions at their current real value.
It turns out that the long-term forecast for UK productivity growth is something like 2.1%, much higher than this minimum and more than enough to maintain the real value of pensions in this simple model without changing the saving or tax ratios.
This confuses me. If productivity does grow as predicted, then there will be no `pensions crisis', since the increased per capita output of the economy will compensate for the decreased number of workers. Pensions will, in real terms, be smaller as a proportion of wages than they are now, but it's not obvious how much that matters.
More here when I've done some more research.